Android OpenGL ES 2.0 的矩阵和坐标到底是怎么一回事儿?
最近依然在研读OpenGL ES 2.0 for Android。在此记录有关Orthographic Matrix、Perspective Matrix、Perspective Divide、Homogeneous Coordinates等各种问答。
理解粗浅,若有错误,还望指正。不过估计没人看这个网站吧。
Q: 为什么OpenGL中的坐标在x、y、z之外还有一个w?
A: 一个原因是3x3矩阵无法完成矩阵三维坐标的位移(同理,2x2矩阵无法完成二维坐标位移),所以给矩阵增加一维,右下角设置为1,其余增加的位置设置为0。这样完成位移后,再把增加的维度去掉,位移完成。在这里w总是1。即使不是1,也会用除法把它变为1,好让最后去掉它(这一步除法叫做Perspective Divide)。
1 | [x 0 0 0] |
增加维度的这种方法就是Homogeneous Coordinates。
参考了The True Power of the Matrix (Transformations in Graphics) - Computerphile。
另外一个原因涉及了三维空间在二维的投影,w会出现不为1的情况。之后讨论。
Q: 为什么android.graphics.Matrix用9个Float,而不是和OpenGL一样用16个?
A: android.graphics.Matrix主要处理2D图像,所以增加了新维度后,矩阵成为了3x3=9个Float。
Q: 为什么andnroid.graphics.Camera可以用android.graphics.Matrix模拟3D效果?
A: Skia的C++看到头疼。注意到其实现中使用了4x4矩阵,所以我猜测andnroid.graphics.Camera替开发者进行了2D->3D->2D的转换。
Q: Orthographic Projection是个啥?
A: 是一个坐标变换矩阵,一次位移 + 一次缩放。
OpenGL需要每个顶点的坐标都在[-1, 1]中,也就是3D空间中位于原点的,边长为2的正方体。
但在设计3D场景(或使用3D设计2D场景)时,如果事先就用正方体中的小数坐标,会很繁琐。而直接用最直观的坐标,比如整数坐标就很方便(也可以是其他范围的坐标,比如正数总比负数好处理吧),但代价是要把这些坐标变换到正方体中。
Orthographic Projection就是这个变换。通过指定我们方便使用的坐标的范围,生成这个矩阵。之后我们把方便使用的坐标和该矩阵相乘,计算机会得出该坐标在正方体中的小数坐标。

Source: https://en.wikipedia.org/wiki/Orthographic_projection
简单地说,矩阵帮我们把设计中的坐标移动到了正方体中,可以让OpenGL显示。
OpenGL ES 2.0 for Android是在解决屏幕长宽的过程中引入了这个概念,有些混乱。这里再解释一下。
用书中的例子,我们要在各种比例的屏幕中放一个圆。如果把横竖位置都设置为[-1, 1],就会挤满整个屏幕,成为了椭圆。这里其实有两个解决方案:
- 根据屏幕修改坐标。这是最直观的想法。在例子中1:1.78的屏幕上,把顶部和底部坐标减小。横屏同理。
- 根据屏幕修改范围。这是书中的思路。坐标依然是[-1, 1],但坐标范围变为了[-1.78, 1.78]。横屏同理。这里我们就可以用Orthographic Projection来把[-1.78, 1.78]范围内的坐标换到正方体中的[-1, 1]中。
参考了The Math behind (most) 3D games - Perspective Projection。之后的内容也会参考这个视频。
Q: Perspective Matrix和Homogeneous Coordinates是个啥?
A: 突出一个抽象。上文的提到的视频很有用。
这里有一个没人跟我说的小秘密。
人眼看到的图像总是二维的,而人眼观察3D世界的视角是砍去一部分顶部的金字塔形状(Frustum,平截头体,截头锥体)。
我站在三维坐标的原点向一个轴看,看到的并不是轴的一个截面,而是把那个金字塔形状戴在头上😳,看到的那个截面。这样才符合现实规则。
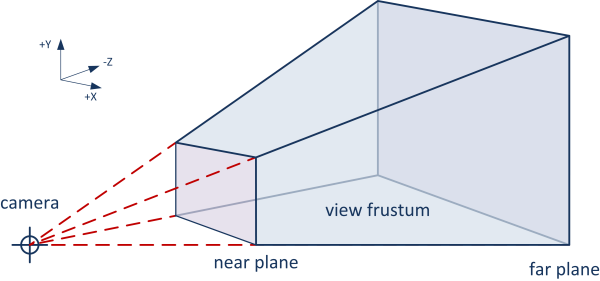
Source: https://learnopengl.com/Guest-Articles/2021/Scene/Frustum-Culling
人眼看到的是near plane大小的图像,其内容是3D空间中把far plane到near plane所有物体从远到近挤到near plane(二维化)的效果。
相关教程中总提距离越远物体越小。实际上物体大小没变,只是在二维化后,距离越远,物体看起来越小,或者说物体是在near plane中越小。
这些浅显的道理放在代码和数学中就会很不直观。
Perspective Matrix的作用是把3D中排好的物体,变化为near plane上的2D坐标。
虽然2D坐标没有z坐标(或者说都相等),但我们需要保留z坐标的相对关系,来确定2D图像中,谁挡住谁。
而在Perspective Matrix的计算中,会出现w不为1的情况。
到这一步,从实用角度来说,我们完全可以忽略工具数儿w了。
编不下去了,到现在我也无法直观地想象出w在3D空间中的样子。